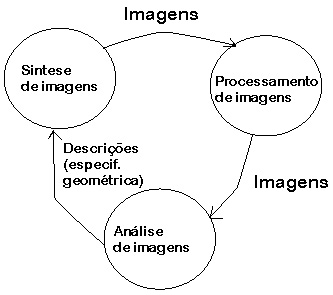
A figura 1.1 apresenta o relacionamento entre as 3 subáreas da Computação Gráfica.
1. Introdução à Computação Gráfica
A Computação Gráfica é a área da ciência da computação que estuda a geração, manipulação e interpretação de modelos e imagens de objetos utilizando computador. Tais modelos vêm de uma variedade de disciplinas, como física, matemática, engenharia, arquitetura, etc.
Pode-se subdividir a Computação Gráfica em 3 sub-áreas [PER89]:
Síntese
de Imagens: sub-área que se preocupa com a produção de representações
visuais a partir das especificações geométrica e visual de seus componentes. É
frequentemente confundida com a própria Computação Gráfica. As imagens
produzidas por esta sub-área são colocadas nos chamados Display-File.
Processamento de Imagens: envolve as técnicas de transformação de Imagens, em que tanto a imagem original quanto a imagem resultado apresentam-se sob uma representação visual (geralmente matricial). Estas transformações visam melhorar as características visuais da imagem (aumentar contraste, foco, ou mesmo diminuir ruídos e/ou distorções). As imagens produzidas/utilizadas por esta sub-área são colocadas/recuperadas nos chamados Raster-File.
Análise de Imagens: sub-área que procura obter a especificação dos componentes de uma imagem a partir de sua representação visual. Ou seja através da informação pictórica da imagem (a própria imagem!) produz uma informação não pictórica da imagem (por exemplo, as primitivas geométricas elementares que a compõem).

A figura 1.1 apresenta o relacionamento entre as 3 subáreas da Computação Gráfica.
Na última década adicionou-se a esse contexto a área de Visualização de
Dados, também chamada Visualização Computacional [Min 97][Sch96], que
usa técnicas de Computação Gráfica para representar informação, de forma a
facilitar o entendimento de conjuntos de dados numéricos de alta complexidade.
Exemplos de áreas de aplicação são: visualização de imagens médicas,
meteorologia, dados financeiros, visualização de programas, dinâmica dos
fluidos, e muitas outras. Nelas, o que existe em comum é que a representação
gráfica (superfícies, partículas, ícones) são geradas automaticamente a partir
do conjunto de dados. Ao usuário cabe definir parâmetros e atributos da imagem
para melhor 'navegar' seu conjunto de dados. Dessa maneira, a visualização de
dados partilha de características da síntese, do processamento e da análise de
dados.
Atualmente a Computação Gráfica é altamente interativa: o usuário
controla o conteúdo, a estrutura e a aparência dos objetos e suas imagens
visualizadas na tela, usando dispositivos como o teclado e o mouse. Entretanto,
até o início dos anos 80, a computação gráfica era uma disciplina restrita e
altamente especializada. Devido principalmente ao alto custo do hardware, poucos
programas aplicativos exploravam gráficos. O advento dos computadores pessoais
de baixo custo, como o IBM-PC e o Apple Macintosh, com terminais gráficos de
varredura (raster graphics displays), popularizou o uso de gráficos na interação
usuário-computador.
Os displays gráficos de baixo custo possibilitaram o
desenvolvimento de inúmeros aplicativos baratos e fáceis de usar, que dispunham
de interfaces gráficas - planilhas, processadores de texto, programas de
desenho... As interfaces evoluiram e introduziu-se o conceito de desktop - uma
metáfora para uma mesa de trabalho. Nessas interfaces gráficas, através de um
gerenciador de janelas (window manager) o usuário pode criar e posicionar
janelas que atuam como terminais virtuais, cada qual executando aplicativos
independentemente. Isto permite que o usuário execute vários aplicativos
simultaneamente, e selecione um deles a um simples toque no mouse. Ícones
(icons) são usados para representar arquivos de dados, programas e abstrações de
objetos de um escritório - como arquivos, caixas de correio (mailboxes),
impressoras, latas de lixo - nas quais são executadas operações análogas às da
vida real. Para ativar os programas, o usuário pode selecionar ícones, ou usar
buttons e menus dinâmicos. Objetos são manipulados diretamente através de
operações de pointing e clicking feitas com o mouse. Atualmente, mesmo
aplicativos que manipulam texto (como processadores de texto) ou dados numéricos
(como planilhas) usam interfaces desse tipo, reduzindo sensivelmente a interação
textual através de teclados alfanuméricos.
A computação gráfica não é mais
uma raridade: é parte essencial de qualquer interface com o usuário, é
indispensável para a visualização de dados em 2D e 3D e tem aplicações em áreas
como educação, ciências, engenharia, medicina, publicidade, lazer, militar,
...
A computação gráfica cuida da síntese de imagens de objetos reais ou
imaginários a partir de modelos computacionais. Processamento de imagens é uma
área relacionada que trata do processo inverso: a análise de cenas, ou a
reconstrução de modelos de objetos 2D ou 3D a partir de suas imagens.
Note
que a síntese de imagens parte da descrição de objetos tais como segmentos de
reta, polígonos, poliedros, esferas, etc.; e produz uma imagem que atende a
certas especificações e que pode, em última instância, ser visualizada em algum
dispositivo (terminal de vídeo, plotter, impressora, filme fotográfico...). As
imagens em questão constituem uma representação visual de objetos bi- ou
tri-dimensionais descritos através de especificações abstratas.
O
processamento de imagens parte de imagens já prontas para serem visualizadas, as
quais são transferidas para o computador por mecanismos diversos - digitalização
de fotos, tomadas de uma câmera de vídeo, ou imagens de satélite - para serem
manipuladas visando diferentes objetivos.
1.1 Sistemas Gráficos
A Computação Gráfica (especialmente as partes relativas a gráficos 3D e a gráficos 3D interativos) desenvolveu-se de modo bem diverso: de simples programas gráficos para computadores pessoais à programas de modelagem e de visualização em workstations e supercomputadores. Como o interesse em CG cresceu, é importante escrever aplicações que possam rodar em diferentes plataformas. Um padrão para desenvolvimento de programas gráficos facilita esta tarefa eliminando a necessidade de escrever código para um driver gráfico distinto para cada plataforma na qual a aplicação deve rodar. Para de padronizar a construção de aplicativos que se utilizam de recursos gráficos e torná-los o mais independentes possível de máquinas, e portanto facilmente portáveis, foram desenvolvidos os chamados Sistemas Gráficos.
Vários padrões tiveram sucesso integrando domínios específicos. Por exemplo, a linguagem Postscript que se tornou um padrão por facilitar a publicação de documentos estáticos contendo gráficos 2D e textos. Outro exemplo é o sistema XWindow, que se tornou padrão para o desenvolvimento de interfaces gráficas 2D em workstations UNIX. Um programador usa o X para obter uma janela em um display gráfico no qual um texto ou um gráfico 2D pode ser desenhado. A adoção de X pela maioria dos fabricantes de workstation significa que um único programa desenvolvido em X pode ser rodado em uma variedade de workstation simplesmente recompilando o código. Outra facilidade do X é o uso de redes de computadores: um programa pode rodar em uma workstation e ler a entrada e ser exibido em outra workstation, mesmo de outro fabricante.
Para gráficos 3D foram propostos vários padrões. A primeira tentativa foi o Sistema Core - Core Graphics System - (1977 e 1979) pelos americanos. Mas a primeira especificação gráfica realmente padronizada foi o GKS - Graphical Kernel System, pela ANSI e ISO em 1985. O GKS é uma versão mais elaborada que o Core. O GKS suporta um conjunto de primitivas gráficas interrelacionadas, tais como: desenho de linhas, polígonos, caracteres, etc., bem como seus atributos. Mas não suporta agrupamentos de primitivas hierárquicas de estruturas 3D. Um sistema relativamente famoso é PHIGS (Programmer’s Hierarchical Interactive Graphics System). Baseado no GKS, PHIGS é um padrão ANSI. PHIGS (e seu descendente, PHIGS+) provêem meios para manipular e desenhar objetos 3D encapsulando descrições de objetos e atributos em uma display list. A display list é utilizada quando o objeto é exibido ou manipulado, uma vantagem é a possibilidade de descrever um objeto complexo uma única vez mesmo exibindo-o várias vezes. Isto é especialmente importante se o objeto a ser exibido deve ser transmitido por uma rede de computadores. Uma desvantagem da display list é a necessidade de um esforço considerável para reespecificar um objeto que está sendo modelado interativamente pelo usuário. Uma desvantagem do PHIGS e PHIGS+ (e GKS) é que eles não têm suporte a recursos avançados como mapeamento de textura.
O XWindow ganhou uma extensão para o PHIGS, conhecida como PEX ,de modo que o X pudesse manipular e desenhar objetos 3D. Entre outras extensões, PEX soma modo imediato ao PHIGS, assim um objeto pode ser exibido durante a sua definição sem a necessidade da display list. PEX também não suporta recursos avançados e só está disponível aos usuários do XWindow.
Um sistema gráfico que tem se tornado bem popular é o OpenGL (GL - Graphics Library) que provê características avançadas e pode ser utilizador em modo imediato ou com display list. OpenGL é um padrão relativamente novo (sua primeira versão é de 1992) e é baseado na biblioteca GL das workstations IRIS da Silicon Graphics. Atualmente um consórcio de industrias é responsável pela gerenciamento da evolução do OpenGL. Existe uma implementação livre (código fonte disponível) do OpenGL conhecida com MesaGL ou Mesa3D.
Como os outros sistemas gráficos, OpenGL oferece uma interface entre o software e o hardware gráfico. A interface consiste em um conjunto de procedimentos e funções que permitem a um programador especificar os objetos e as operações que os envolvem produzindo imagens de alta qualidade. Como o PEX, o OpenGL integra a manipulação de objetos 3D desenho ao X, mas também pode ser integrado em outros sistemas de janela (por exemplo, Windows/NT) ou pode ser usado sem um sistema de janela. OpenGL provê controle direto sobre operações gráficas fundamentais em 3D e 2D. Incluindo a especificação de parâmetros como matrizes de transformação e coeficientes de iluminação, métodos de antialiasing e operações sobre pixels, mas não provê mecanismos para descrever ou modelar objetos geométricos complexos.
1.2 Aplicações da CG
A lista de aplicações é enorme, e cresce rapidamente. Uma amostra significativa inclui:
Traçado interativo de gráficos: aplicativos voltados para usuários em ciência, tecnologia e negócios geram gráficos que ajudam na tomada de decisões, esclarecem fenômenos complexos e representam conjuntos de dados de forma clara e concisa.
Automação de escritórios e editoração eletrônica: o uso de gráficos na disseminação de informações cresceu muito depois do surgimento de software para editoração eletrônica em computadores pessoais. Este tipo de software permite a criação de documentos que combinam texto, tabelas e gráficos - os quais tanto podem ser "desenhados" pelo usuário ou obtidos a partir de imagens digitalizadas.
Projeto e desenho auxiliado por computador: em CAD, sistemas gráficos interativos são utilizados para projetar componentes, peças e sistemas de dispositivos mecânicos, elétricos, eletro-mecânicos e eletrônicos. Isto inclui edifícios, carcaças de automóveis, aviões e navios, chips VLSI, sistemas óticos, redes telefônicas e de computador. Eventualmente, o usuário deseja apenas produzir desenhos precisos de componentes e peças. Mais frequentemente, o objetivo é interagir com um modelo computacional do componente ou sistema sendo projetado, de forma a testar propriedades estruturais, elétricas ou térmicas, até atingir um projeto satisfatório.
Simulação e animação para visualização científica, lazer, arte e publicidade: uma das áreas que mais evoluiram na década de 80 foi a visualização científica. Cientistas e engenheiros perceberam que não poderiam interpretar as quantidades prodigiosas de dados produzidas por programas em supercomputadores sem resumir os dados e identificar tendências e fenômenos através de representações gráficas. Como resultado, surgiram animações computadorizadas do comportamento variante no tempo de objetos reais ou simulados. Tais animações podem ser utilizadas para estudar entidades matemáticas abstratas e modelos matemáticos de fenômenos como fluxo de fluidos, relatividade, reações químicas e nucleares, deformação de estruturas mecânicas sob diferente tipos de pressão, etc. Outras aplicações tecnológicas avançadas incluem a produção de desenhos animados e efeitos especiais para filmes e comerciais de TV, que requerem mecanismos sofisticados para modelar objetos e para representar luz e sombra.
Controle de processos: sistemas de controle de tráfego aéreo e espacial, sistemas de controle de refinarias e de usinas de energia mostram graficamnente os dados coletados por sensores conectados a componentes críticos dos sistemas, de forma que os operadores possam responder adequadamente a condições críticas.
Cartografia: a computação gráfica é usada para produzir representações precisas e esquemáticas de fenômenos naturais e geográficos obtidos a partir da coleta de dados.
Arte: A arte por computador vem crescendo imensamente nos últimos anos.É possível utilizar novos recursos de computação gráfica para produzir efeitos artísticos, como a extração de texturas, padrões e estruturas a partir de fotos digitalizadas.
Gráficos de Apresentação (Presentation Graphics): É a utilização de técnicas gráficas para demonstração de resultados, idéias e gráficos, com o intuito de mostrar ou transmitir conhecimento específico como, por exemplo, em uma aula, ou reunião, ou na contrução de material didático.
Neste curso, estamos interessados principalmente em técnicas de síntese de imagens bem como seu relacionamento com o processamento de imagens. Também não pretendemos explorar todo o escopo de aplicações da CG, mas estudar os conceitos gerais envolvidos na programação das primitivas gráficas que estão por trás dessas aplicações.
1.3 Hardware Gráfico

Figura 1.2: Sistemas de hardware para computação gráficas.
Um sistema de hardware para computação gráfica consiste essencialmente de
dispositivos gráficos de entrada e saída (I/O) ligados a um computador (Fig.
1.2). Ao conjunto de dispositivos de I/O gráficos alocados para utilização por
uma única pessoa por vez denomina-se genericamente de "estação de trabalho
gráfica", ou graphics workstation. Um sistema gráfico multiusuário pode ter
várias estações gráficas, de forma que mais de um dos vários dispositivos de I/O
disponíveis podem estar conectados e utilizando o computador hospedeiro. Como na
CG é frequente a manipulação de grandes quantidades de dados, o computador deve
ser equipado de memória secundária com alta capacidade de armazenagem. Além
disso, um canal de comunicação de alta velocidade é necessário para reduzir os
tempos de espera. Isto normalmente é feito através de comunicação local sobre um
barramento paralelo com velocidade de transmissão de dados da ordem de um milhão
de bits por segundo. Se o equipamento gráfico está distante do processador
(conexão remota), um canal de comunicação serial pode ser necessário.
Transmissão serial assíncrona pode ser feita a velocidades de até 19.2 kbps
(milhares de bits por segundo). Mesmo tal velocidade pode ser muito lenta para
alguns objetivos como animação gráfica de alta resolução, onde cada frame de
imagem pode ter um megabyte de dados. Um sistema de conexão ideal nesse caso é
uma Local Area Network (LAN) como a Ethernet.
Os dispositivos de saída
gráficos podem ser de natureza digital ou analógica, resultando em duas classes
de gráficos, denominados vector graphics (gráficos vetoriais), que desenham
figuras traçando sequências de segmentos de reta (vetores); e raster graphics
(gráficos de varredura, ou matriciais), que desenham figuras pelo preenchimento
de uma matriz de pontos (pixels).
1.4 Resolução Gráfica
Virtualmente todos os dispositivos de I/O gráficos usam uma malha retangular
de posições endereçáveis - a qual é denominada "retângulo de visualização" ou "envelope". A
"resolução gráfica" de um dispositivo é o número de posições (ou pontos, ou
pixels) horizontais e verticais que ele pode distinguir. Existem 4 parâmetros
que definem a resolução:
1. ndh - o número de posições endereçáveis horizontalmente.
2. ndv - o
número de posições endereçáveis verticalmente.
3. width - a largura do
retângulo de visualização em mm.
4. height - a altura do retângulo de
visualização em mm.
A partir desses 4 parâmetros, vários números interessantes podem ser calculados:
1. resolução horizontal: horiz_res:= ndh/width
2. tamanho ponto
horizontal: horiz_dot_size:= width/ndh
3. resolução vertical:
vert_res:= ndv/height
4. tamanho ponto vertical: vert_dot_size:=
height/ndv
5. total pontos endereçáveis: total_nr_dots:= ndh*ndv
6.
resolução de área: area_res:= total_nr_dots/(width*height)
7. razão
de aspecto gráfica: aspect_ratio:= vert_dot_size/horiz_dot_size
8.
razão de aspecto física: physical_aspect_ratio:= height/width
Obs:
O ideal seria ter um aspect ratio igual ou próximo de 1.
1.5 Sistemas de Coordenadas
Na CG é necessário definir sistemas de coordenadas para quantificar os dados sendo manipulados. Já vimos que os dispositivos de visualização gráfica matriciais consistem de uma matriz de pixels endereçáveis, e um gráfico é formado "acendendo" ou "apagando" um pixel. Os pixels são endereçados por dois números inteiros que dão suas coordenadas horizontal e vertical, dcx, e dcy, respectivamente, onde:
Eq.(1.1)
Na matriz de pixels, o valor dcx+1 dá o número da coluna, e dcy+1 dá o número
da linha do pixel endereçado. O pixel endereçado como (0,0) está geralmente no
canto inferior esquerdo do retângulo de visualização. As coordenadas (dcx,dcy)
são chamadas de coordenadas do dispositivo, e podem assumir apenas valores
inteiros.
Coordenadas do dispositivo podem variar bastante para diferentes
equipamentos, o que levou à utilização de coordenadas normalizadas do
dispositivo (NDC - normalized device coordinates), para efeito de padronização
(ndcx,ndcy). NDCs são variáveis reais, geralmente definidas no intervalo de 0 a
1:
Eq. (1.2)
A coordenada NDC (0,0) corresponde à origem (0,0) nas cordenadas do
dispositivo, e a coordenada NDC (1,1) refere-se ao pixel no canto superior
direito, que corresponde ao pixel (ndhm1,ndvm1) nas coordenadas do
dispositivo.
A vantagem da utilização de NDCs é que padrões gráficos podem
ser discutidos usando um sistema de coordenadas independente de dispositivos
gráficos específicos. Obviamente, os dados gráficos precisam ser transformados
do sistema de coordenadas independente para o sistema de coordenadas do
dispositivo no momento de visualização. O mapeamento de NDCs (reais) para
coordenadas do dispositivo (inteiros) é "linear", por exemplo:
Eq. (1.3)
Dois outros sistemas de coordenadas são úteis. O primeiro é o sistema de cordenadas físico, (pcx,pcy) onde pcx é a distância física ao longo do eixo x a partir do extremo esquerdo do retângulo de visualização, e pcy é a distância física ao longo do eixo y a partir do extremo inferior. As unidades de medida utilizadas são polegadas ou milímetros. A transformação de coordenadas físicas para coordenadas do dispositivo é dada por:
Eq. (1.4)
O segundo é o sistema de coordenadas do mundo, ou sistema de coordenadas do usuário, que consiste de coordenadas cartesianas (x,y), num intervalo qualquer definido pelo usuário:
Eq. (1.5)
Os parâmetros que definem o intervalo de valores de x e y, xmin, ymin, xmax e ymax, definem uma área retangular no espaço bidimensional, denominada de janela. A transformação de coordenadas do usuário (x,y) para NDCs (ndcx,ndcy), denominada transformação de visualização, é dada por:
Eq. (1.6)
Para visualizar dados num dispositivo gráfico qualquer, é necessário transformá-los das coordenadas do usuário para NDCs, e de NDCs para coorde-nadas do dispositivo. Da mesma forma, dados de entrada gráficos precisam ser transformados de coordenadas do dispositivo para NDCs, e depois para coordenadas do usuário (Fig. 1.3).
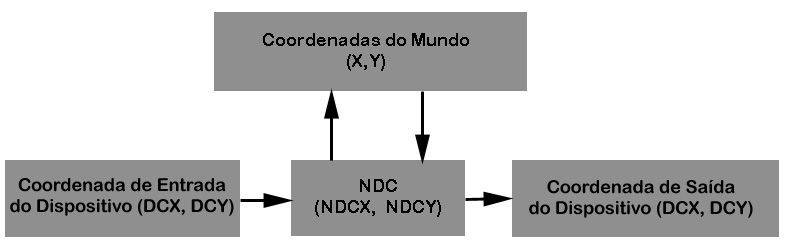
Figura 1.3: Sistemas de coordenadas e suas transformações.
1.6 Exercícios
1. Escreva os procedimentos "inp_to_ndc", "ndc_to_user", "user_to_ndc" e
"ndc_to_user", que transformam dados entre os vários sistemas de coordenadas,
conforme ilustrado na Fig. 1.2. Repita o exercício assumindo que o intervalo de
variação do sistema NDC vai de:
(i) -1 a +1 (coordenadas normalizadas
centradas)
(ii) 0 a 100
1.7 Bibliografia
[FOL90] Foley, James D. et al : Computer Graphics - Principles and Practice, Addison-Wesley Publishing Company, 1990.
[MIN97] Minghim, R; Oliveira, M. C. F. Uma Introdução à Visualização Computacional XVI JAI’97, Jornadas de Atualização em Informática, XVII Congresso da SBC, Brasília, agosto de 1997, Cap. 3, pp. 85-131.
[PER89] Persiano, R.C.M.; Oliveira, A.A.F. :Introdução à Computação Gráfica, Livros Técnicos e Científicos Editora Ltda., 1989.
[SCH96] Schröeder, W.J.; Martin, K.; Lorensen, W. - The Visualization Toolkit - An Object-Oriented Approach to 3D Graphics, Prentice-Hall, 1996.
[SEG98] Segal, M.; Akeley, K. - The OpenGL Graphics Interface; SIGGRAPH’98 Course Notes.
[Woo97] Woo, M.; Neider, J.; Davis, T.; - OpenGL Programming Guide. Second Edition, Addison Wesley, 1997.